Delaunay Triangulation using Parallel Incremental Extrapolation on GPUs
CS205 Final Project, Fall 2011
Introduction
We develop a method for constructing the Delaunay triangulation of a point set which is massively parallel and designed for the many-core architecture of graphical processing units (GPUs). We implement a "parallel incremental extrapolation" algorithm on the plane (2D) under the general position assumption and measure promising speedup with respect to our naive serial implementation.
Motivation
Our choice of project is motivated by the new hydrodynamics simulation code AREPO used by our research group in the Astronomy department. This code is a finite volume scheme defined on an unstructured, moving mesh which is defined by the Voronoi tessellation of a set of discrete points. This method has been shown to have several advantages over both static finite volume methods (e.g. Adaptive Mesh Refinement/AMR) as well as finite mass methods (Smoothed Particle Hydrodynamics/SPH), the other main schemes used in astrophysics simulations.
Mesh construction and update is a large computational expense for the code, since the Voronoi tessellation must be generated every timestep. In recent cosmological simulations (Vogelsberger et al. 2011) the mesh was the most expensive component of the CPU usage. This makes it an ideal target for optimization. For our final project, our aim was to implement a parallel Delaunay triangulation (the toplogical dual of the Voronoi diagram) algorithm accelerated by the recent explosion in the computational power of graphical processing units (GPUs).
The ultimate goal - an efficient and robust CUDA implementation of Delaunay triangulation in 3D - is out of scope of this assignment. We therefore focus on a data-parallel algorithm for Delaunay triangulation, aiming to accelerate parts of the algorithm using CUDA. We propose an algorithm modeled after that described in Teng et al. (1993) which we call "Parallel Incremental Extrapolation" (PIE).
Our Approach
This project is focused on the implementation of an “exact” Voronoi tessellation for a discrete point set. The topological dual of the Voronoi tessellation is the Delaunay triangulation. In general, it is easier to construct the Delaunay triangulation and then obtain the corresponding Voronoi diagram. A few groups have attempted Delaunay implementations on the GPU which utilize the calculation of the “discrete Voronoi tessellation” (DVT), using, for example, the jump flooding algorithm. However, this approach is applicable particularly to uniform random distributions of points, and not to the highly clustered distributions of points likely to be found in our applications.
We instead model our approach on the "incremental construction" class of algorithms, which to our knowledge have not yet been attempted on the GPU. We describe the serial algorithm in two dimensions:
- 1. Locate a starting vertex (for instance, closest to the center of the box).
- 2. Find the first Delaunay edge by gift wrapping / locating the closest point.
- 3. Initialize the open edge list (OEL) to the initial edges.
- 4. While the OEL is not empty:
- 4a. expand all open edges into triangles by locating the third point such that the resulting circumcircle contains no other points.
- 4b. Append the new triangles to a triangle list (TL)
- 4c. Append the new (oriented) edges to the OEL
- 4d. Cleanup: remove duplicates and opposite-duplicates in the OEL
Since all the open edge expansions can be done independently, this step can be done in parallel. Furthermore, instead of starting the construction from a single central point and extrapolating outward, we can start the construction from all points in the entire domain simultaneously. This data-parallel approach seems particularly suited for the GPU architecture. In general, we assign one thread per open edge (which number a significant fraction of N, the total number of points, for each iteration). For large N, this allows us to fully saturate the GPU with a large number of threads.
An important caveat is that for efficient point searches we need some form of acceleration structure. In the original Teng et al. paper uniform bucketing was used. We would implement, instead, a quadtree or octtree in 3D. However, implementation of such an acceleration structure on the GPU is an added level of difficulty and we do not include it in our initial implementation.
If the depth of a triangle is defined as the number of neighbor hops from the initial OEL, it has been shown that this algorithm performs a breadth-first search of the Delaunay graph. So, all triangles will be discovered in a finite number of iterations of step (4). In practice this value is likely to be between 5-10. We implement step (4) as a series of CUDA kernels which are then typically run for a small number of iterations until the OEL is empty and the triangulation is complete. The TL is then transfered back to the host and either (a) visualized (in the case of our project example code); or (b) used to construct the voronoi polyhedra for the hydrodynamics simulation (in the case of the the application usage scenario).
Results
Verification
We implement the above algorithm in a simple proof of concept C program which reads input data sets from a flat text file, computes the Delaunay triangulation both in serial and in parallel on the GPU, and writes out a simple form of the tesellation structure.
We directly compare the results of our GPU-based algorithm to the existing serial algorithm. Our parallel and serial implementations produce identical triangulations for our trial point sets (luckily!). Small, "testing" data sets allow us to evaluate by eye the validity of the results during the debugging process. Some examples of triangulations are shown below.
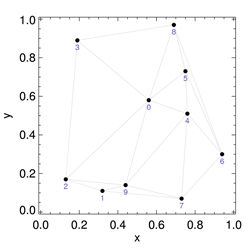
Figure 1. Three examples Delaunay triangulations of point sets in the plane (2D) in general position generated by our approach, with N=10, N=322, and N=1282 point.
Performance
Our main goal is a working algorithm that does part of the computation on a GPU, and in doing so achieves a speedup > 1 compared to the serial version of the same algorithm. This problem has a high parallelization potential. The CPU incremental insertion algorithm currently used in AREPO achieves N log N scaling for a random point set. The parallel extrapolation technique should exhibit O(N) scaling for the edge expansion phase and O(1) scaling for the point search for each site, although this will require acceleration techniques for nearest point searches. Our test implementation is brute force and so we expect O(N) scaling for the point search as well.
We measure several metrics to gauge performance. Our benchmark system has (2) Intel Xeon X5650 Westmere 2.66 Ghz 6-Core CPUs, (6) 8GB DDR3 1333 Mhz ECC memory for 48GB total, and (2) Nvidia Tesla C2070 GPUs each at 1.15 Ghz 14 SM (448 cores) with 6GB RAM. For all of our testing we compare single-core performance of the Xeon to single-card performance of one C2070. In our GPU timings we also always include all memory transfers to and from the host.
First, Figure 2 presents the speedup of the GPU accelerated algorithm relative to our otherwise identical serial implementation on the CPU. In the case where the "cleanup" phase remains on the CPU (our first attempt), additional memory transfer overhead and CPU-based array duplicate removal and compaction leads to an asymptotic speedup of a few. Rewriting the majority of the cleanup as a GPU kernel (although we leave the OEL compaction on the host for now) allows us to skip unnecessary memory transfers and perform the duplicate checks more quickly. In this case we reach large speedups of > 10 as the point set size grows larger. However, the strong caveat is that we are comparing our highly unoptimal serial implementation to our GPU method. State of the art serial tesellators optimized for the CPU will not only greatly outperform our implementation by large margins, they will also scale better with the point set size. Thus, our measured speedup is more an indication of the parallelization potential of the "incremental construction" approach to Delaunay triangulation, rather than an indication of real world performance.
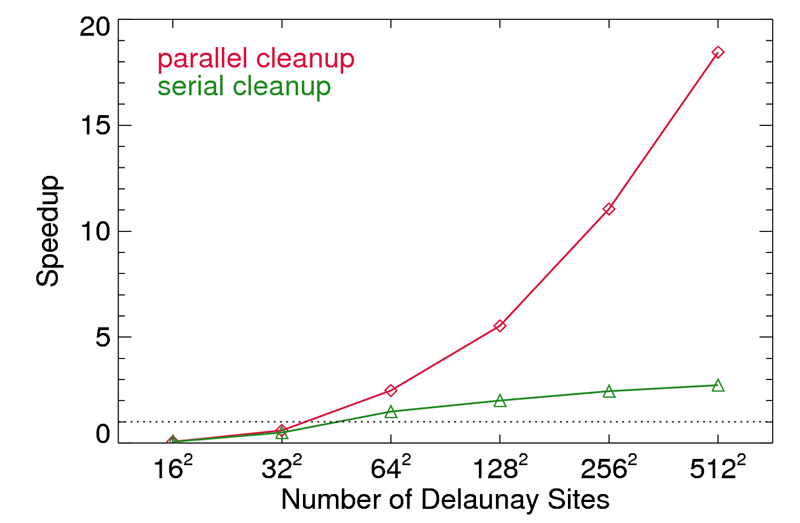
Figure 2. Speedup of the GPU accelerated algorithm relative to our serial implementation. The two different lines indicate if the duplicate check and removal phase ("cleanup") is done on the CPU or GPU.
In general, the GPU implementation performs extremely poorly for small N (as expected). The minimum size to hide the kernel launch latency and the memory transfers seems to be around N = 642.
An important source of parallelism in this algorithm is its ability to start from multiple (or all) points simultaneously. Figure 3 shows the same speedup measures at for various numbers of starting points N0 from one to 256. For point sets N > 642 performance monotonically increases with increasing numbers of starting sites. Starting with 162 sites the gain is marginal, which may be indicative of some component not scaling as well as it should. Similarly, for large N0 the speedup appears to be approaching an asymptotic value with increasing point set size. In contrast, starting with only one or four sites seems to avoid this behavoir.
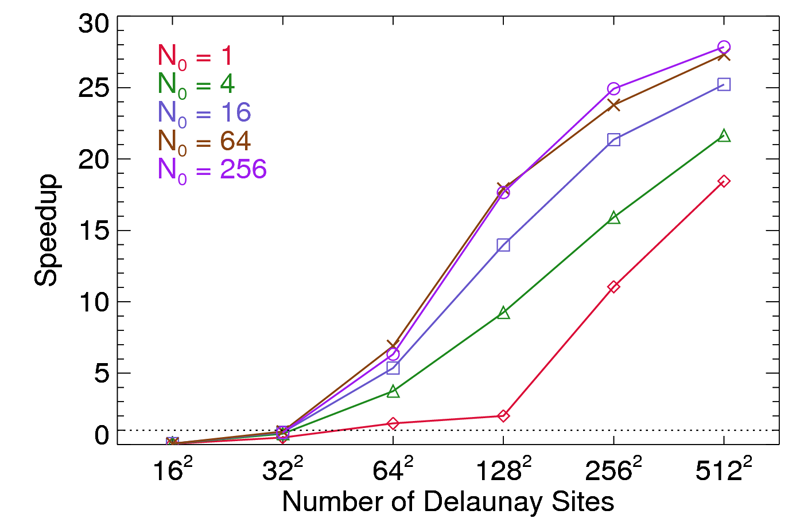
Figure 3. Speedup of the GPU accelerated algorithm relative to our serial implementation, as above. The number of starting sites N0 is varied from one to 256 as indicated by the different colored lines.
The main consequence of the number of starting points is a reduction in the number of open edge expansion iterations. We measure this drop at fixed point set size 1282 in Figure 4. We expect that in the limit of N0 -> N, the number of iterations will approach our best case scenario of 5 - 10, and this does appear to be the case. It will be informative to further explore the case when N0 = N. This mode generates extremely large open edge lists, which although in theory allow the most parallelization potential, may be subject to bottlenecks in our code.
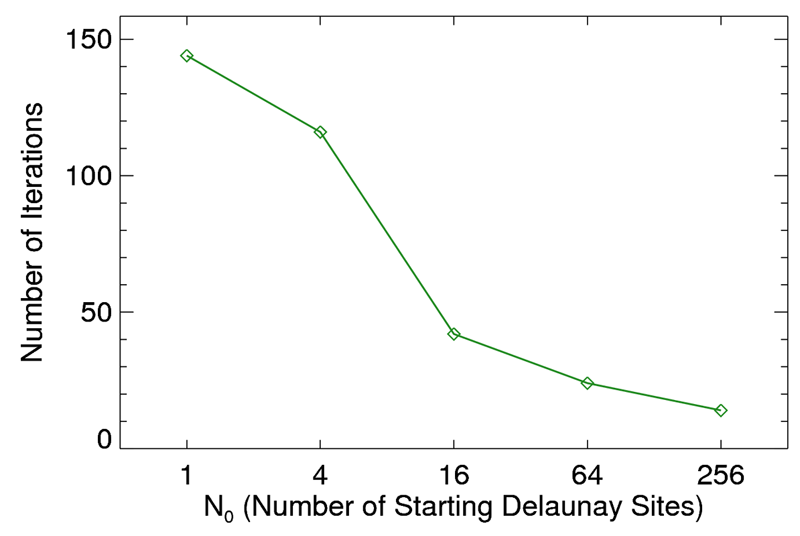
Figure 4. Number of edge expansion iterations as a function of the number of starting sites, for a fixed point set size of N = 1282. We expect that in the limit of N0 -> N, the number of iterations will approach our best case scenario of 5 - 10.
In terms of optimizing the kernel launch configuration (number of threads per block, blocks in each grid) we show in Figure 5 the relative computation time of various TPB settings relative to the case of 32, our nominal value. We include TPB = 8 and 16 just for reference, as we expect the GPU to perform at a quarter or half performance level when individual warps are not full. We find that all configurations run slower than when using just 32 threads per block. That said, the curves are more or less flat (up to a factor of two) up to 512 threads per block. Kernels typically perform better when launching with blocks which each have some multiple of two times 32 threads, in order to help hide memory latency. Our implementation does not benefit in this way. We claim this is due to the general lack of block level optimization (such as efficient use of shared memory structures), as well as a cleanup kernel which is almost entirely dominated by global memory manipulations with minimal arithmetic computation.
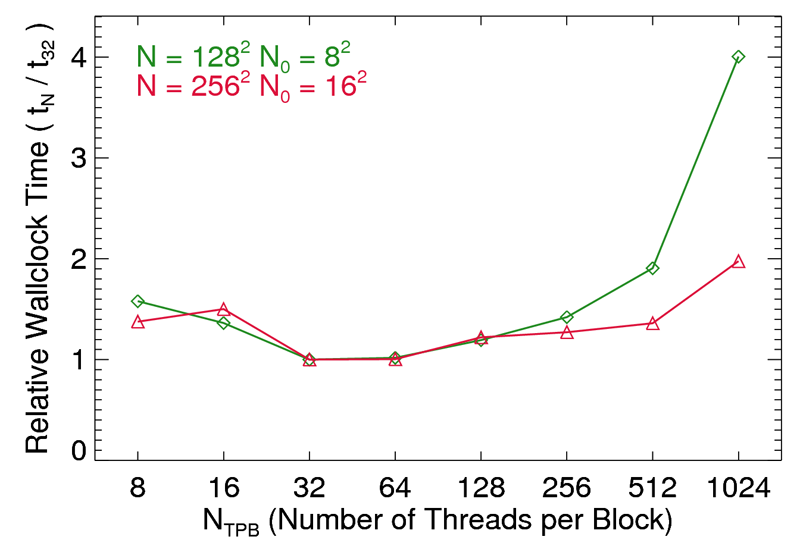
Figure 5. Relative increase in run (wallclock) time as a function of the number of threads assigned per block. Each is normalized to our nominal testing value of 32, which we in fact find to be the optimal configuration.
Conclusions and Future Work
Although the geometric predicates involved in constructing a Delaunay triangulation can be recast in terms of linear algebra operations such as determinants which can be evaluated extremely efficiently on modern hardware, the nature of an unstructured mesh makes its implementation on the data-parallel architecture of a GPU difficult. For maximum efficiency, each thread (of many) must execute the same instructions across an array of input data. Furthermore, access to memory must be both coalesced and minimal.
We discovered that satisfying these constraints when developing an algorithm for Delaunay triangulations on the GPU was quite difficult, as expected. Our implementation, therefore, is more an exploration of the parallelization potential of the "incremental construction" technique, and not a measure of real world performance.
To make our software fully functional for its intended design goal - namely, constructing a mesh during each timestep of a hydrodynamics code, several improvements will need to be made. Of paramount importance is correctness and redundancy against failure. That is, the construction will need to be made robust. Currently this involves the use of exact integer arithmetic via the GMP library. Porting such calculations to the GPU seems an open area of research, although it would likely be more efficient to simply flag degenerate or potentially degenerate cases and have the CPU perform this calculation.
Additionally, to make it competitive with serial point insertion techniques which are highly optimized for CPUs, we have to remove the brute force point search. To this end some sort of acceleration structure is required - bucketing points into groups or tree search. This is also an active area of research on the GPU, and although at first glance tree construction and search seems likely a highly non-optimal problem for the GPU (lots of random memory access), there are several promising studies. It is also possible that the CPU could perform such tree searches and send work units to the GPU which represented only a subset of the domain. These, individually, would be small enough to perform brute force minimum distance searches on the GPU, catering directly to its strength.
If we were starting this project over, we would have considered the cleanup phase more carefully from the start. Most of the complications we ran into turned out to stem from some degenerate case we had not considered in our cleanup function. In addition, the cleanup could be done much more efficiently than currently implemented on the GPU, using scan operations to implement search and compaction. We leave this to future work.
References
Several groups have previously explored Delaunay triangulations on GPUs. The methods fall into two broad categories. The first uses a discrete Voronoi diagram to create an approximation DT followed by a correction step:
- Cao et al. (2010) - Proof of correctness of the digital delaunay triangulation algorithm
- Cao et al. (2011) - Parallel banding algorithm to compute exact distance transform with the GPU
- Qi et al. (2011) - Computing 2D constrained DT using graphics hardware
- Rong et al. (2007) - Jump flooding in GPU with applications to Voronoi diagrams
- Rong et al. (2007) - Variants of JFA for computing discrete voronoi diagrams
- Rong et al. (2008) - Computing 2D Delaunay triangulation using graphic hardware
- Yuan et al. (2011) - Generalized Voronoi diagram computation on the GPU
The second restores an arbitrary triangulation to a DT, though the construction of the initial triangulation must be done separately:
- Navarro et al. (2011) - A quasi-parallel GPU based algorithm for Delaunay edge-flips
- Navarro et al. (2011) - A parallel GPU-based algorithm for Delaunay edge-flips
PhD theses of relevance to meshing on the GPU:
- Rong (2007) - Jump flooding algorithm on GPU and its applications
- Bollig (2009) - Constrained voronoi tesselation of manifolds using the GPU
General research on parallel algorithms for Delaunay triangulation was widespread before the popularity of GPUs:
- Cignoni et al. (1993) - Evaluation of parallelization strategies for incremental insertion in Ed
- Cignoni et al. (1993) - Parallel 3D Delaunay triangulation
- Cignoni et al. (1994) - A merge-first divide and conquer algorithm (DeWall and InCoDe)
- Cignoni et al. (1997) - DeWall - a fast divide and conquer Delaunay triangulation algorithm in Ed
- Isenberg et al. (2006) - Streaming computation of delaunay triangulations
- Lee et al. (1997) - Parallel algorithm for delaunay triangulation
- Teng et al. (1993) - A data-parallel algorithm for 3D Delaunay triangulation
Web links of interest:
- Triangle - fast(est) serial Delaunay triangulator
- GPU-DT - a 2D delaunay triangulation in CUDA (Cao et al. group)
- Streaming Delaunay - large meshes and out of core computation
- Interactive Voronoi - a WebGL applet w/ applications to NNI