Rekonstruktion von Galaxienhaufen mit Hilfe des Linseneffektes

Allgemeines

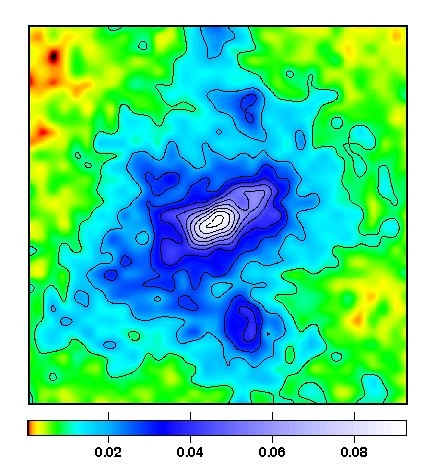Gegenstand unserer Arbeit ist die möglichst genaue Rekonstruktion des Massenprofiles von Galaxienhaufen. Wie schon im allgemeinen Überblick erwähnt, sind Galaxienhaufen sehr wichtige kosmologische Objekte, deren Häufigkeit am Himmel und genaue Masse es zu bestimmen gilt. Der Gravitationslinseneffekt ist unserer Ansicht nach die vielversprechendste Methode hierfür.
Während der starke Linseneffekt eine hochauflösende Rekonstruktion des Galaxienhaufenzentrums ermöglicht, erschließt der schwache Linseneffekt das gesamte Beobachtungsfeld. Eine Kombination aus beiden Effekten, wie wir es mit unserer Methode versuchen, bietet also die Möglichkeit zur Galaxienhaufenrekonstruktion auf allen beobachteten Skalen.

Referenzen

Neben unseren eigenen Veröffentlichungen sind hier auch zwei andere Ansätze zur Kombination von starkem und schwachem Linseneffekt aufgelistet.

• Combining weak and strong lensing in cluster potential reconstruction
  Cacciato, Bartelmann, Meneghetti, Moscardini
  2006, A&A, 458, 349
  [astro-ph]
• Combining weak and strong cluster lensing: Applications to simulations and MS 2137
  Merten, Cacciato, Meneghetti, Mignone, Bartelmann
  2008, submitted to A&A
  [astro-ph]
• Strong and weak lensing united I: the combined strong and weak lensing cluster mass reconstruction method
  Bradač, Schneider, Lombardi, Erben
  2005, A&A, 437, 39
  [astro-ph]
• Combined reconstruction of weak and strong lensing data with WSLAP
  Diego, Tegmark, Protopapas, Sandvik
  2007, MNRAS, 375, 958
  [astro-ph]

Rekonstruktionsmethode

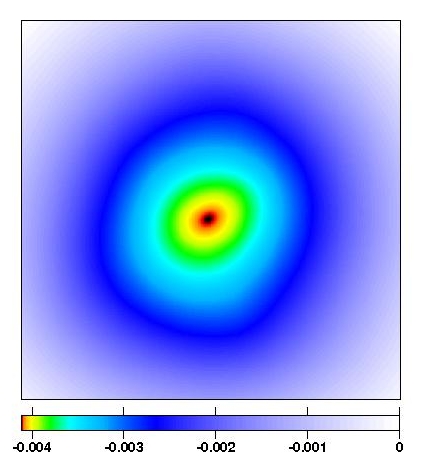Wir haben uns für das Linsenpotential als Rekonstruktionsgröße entschieden. Dabei handelt es sich um das reskalierte und entlang der Sichtlinie integrierte Newtonsche Potential. Der Vorteil dieses Potentials gegenüber direkteren Rekonstruktionsgrößen, wie z.B. der Dichteverteilung, liegt in seiner Gleichmäßigkeit. Diese Eigenschaft macht es sehr stabil gegenüber Rauschen und Ausreißern in den Beobachtungsdaten.
Das Grundprinzip unseres Algorithmus ist eine sog. Maximum-Likelihood-Methode. In Worten beschrieben, versuchen wir jenes Linsenpotential zu finden, welches, gegeben die Beobachtungsdaten, die größte Wahrscheinlichkeit aufweist, die Beobachtungen verursacht zu haben. Dazu teilen wir das Beobachtungsfeld in Pixel auf und erhalten ein reguläres Gitter. Anschließend definieren wir eine Chi-Quadrat-Funktion in jedem Pixel und minimieren sie auf diesem Gitter. Die Größe, bezüglich der minimiert wird, ist das Linsenpotential selbst. Auf diese Art und Weise erhalten wir eine nicht-parametrische Rekonstruktionsmethode, indem wir zusätzlich jedem Pixel auch eine Beobachtungsgröße zuordnen, welche vom Linsenpotential abhängt. Wie diese Chi-Quadrat-Funktion konkret aussieht, erklären wir im nächsten Abschnitt.

Referenzen

Hier eine Referenz zu Maximum-Likelihood basierten Galaxienhaufen-Rekonstruktionsmethoden.

• Maximum-likelihood Cluster Reconstruction
  Bartelmann, Narayan, Seitz, Schneider
  1996, ApJ, 464L, 115B
  [astro-ph]

Verschiedene Linseneffekte

Zum jetzigen Zeitpunkt verarbeiten wir zwei verschiedene Arten von Beobachtungen in unseren Rekonstruktionen.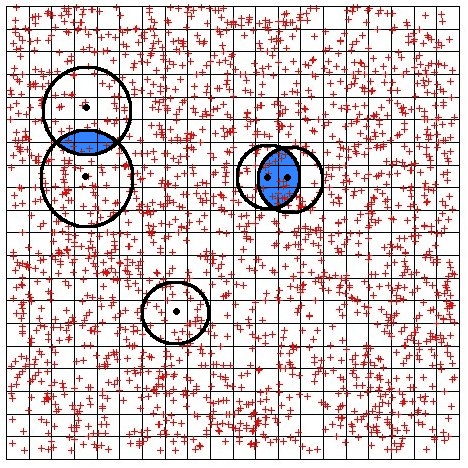 Zum einen ist da der schwache Linseneffekt, also die leicht elliptische Verzerrung von Hintergrundgalaxien. Wie im Abschnitt über Gravitationslinsen beschrieben, muss man diesen Effekt statistisch behandeln, da die Hintergrundgalaxien auch intrinsische Elliptizität tragen. Man kann zeigen, dass der Erwartungswert der Elliptizät gleich der sog. reduzierten Scherung ist, einer charakteristischen Linseneigenschaft, welche von zweiten Ableitungen des Potentials abhängt. Wir haben also die gesuchte Größe zur Definition der Chi-Quadrat-Funktion des schwachen Linseneffektes gefunden. Um die nötige Mittelung über Hintergrundgalaxien auszuführen, werden um jeden Pixel Kreise gezogen, dessen Radius kontinuierlich ansteigt, bis die gewünschte Anzahl an Galaxien (typischerweise 10-15) enthalten ist. Die Radien verschiedener Pixelkreise können dabei durchaus überlappen, dadurch entstehende Korrelationen in der Rekonstruktion werden in Betracht gezogen.
Die Beobachtung, die wir in unserer Methode dem starken Linseneffekt zugrunde legen, sind Bögen. Man kann zeigen, dass diese Bögen bei nicht allzu hoher Auflösung sehr nahe an der sog. kritischen Kurve eines Galaxienhaufens liegen. Dabei handelt es sich um eine andere charakteristische Linseneigenschaft, welche ebenfalls von zweiten Ableitungen des Linsenpotentials abhängt. Für jeden Pixel, der einen Teil eines Bogens enthält, definieren wir also eine zusätzliche Chi-Quadrat-Funktion, die den starken Linseneffekt beinhaltet. Da sich diese Bögen sehr gut beobachten lassen und die Gitterauflösung aufgrund der Mittelung im schwachen Linseneffekt sowieso schon recht gering ist, verwenden wir für diese Pixel eine feinere Gitterauflösung, um keine Information zu verschenken.

Referenzen

Eine detaillierte Beschreibung der Methode, inklusive der fehlenden Formeln ist hier zu finden.

• Combining weak and strong cluster lensing: Applications to simulations and MS 2137
  Merten, Cacciato, Meneghetti, Mignone, Bartelmann
  2008, submitted to A&A
  [astro-ph]

Vorteile unserer Methode

Bevor wir zu etwas technischeren Details unserer Methode kommen, wollen wir noch die wichtigsten Vorteile gegenüber anderen Ansätzen hervorheben.

• Der Vorteil gegenüber Methoden die sich nur auf einen einzigen Linseneffekt beschränken ist offensichtlich. Eine Kombination aus beiden Effekten erlaubt eine Rekonstruktion auf allen Skalen.
• Der Maximum-Likelihood-Ansatz macht die Methode enorm flexibel, da man für sehr viele Beobachtungen Chi-Quadrat-Funktionen definieren kann. Tatsächlich arbeiten wir derzeit daran, unsere Methode mit einem Effekt namens Flexion und der Berücksichtigung von Mehrfachbildern zu erweitern.
• Das adaptive Mittelungsschema für die Hintergrundgalaxien erlaubt Rekonstruktionen mit hoher Auflösung auch bei sehr niedriger Hintergrundgalaxiendichte.
• Die Verwendung von Bögen als Element des starken Linseneffekt ist sehr einfach in der Umsetzung, da diese sehr viel einfach zu beobachten sind als z.B. Mehrfachbilder.

Numerische Umsetzung

Die konkrete technische und numerische Umsetzung der oben beschriebenen Rekonstruktionsmethode ist nicht einfach. Zunächst tauchen in den Chi-Quadrat-Funktionen mehrere v.a. zweite Ableitungen des Linsenpotentials auf. Diese stellen wir durch finite Differenzen auf dem definierten Gitter dar. Auf diese Weise lassen sich die Ableitungen durch einfache Matrixmultiplikationen ausführen. Das Problem daran ist, dass sehr viele Matrixmultiplikationen mit sehr hoher Dimensionalität nötig werden. Glücklicherweise sind diese Matrizen nur relativ dünn besetzte Bandmatrizen, welche sehr spezialisierte und enorm schnelle Multiplikationsalgorithmen zulassen. In der Praxis haben wir durch die Verwendung dieser Algorithmen Geschwindigkeitszugewinne bis zu einem Faktor von 1000 erreicht. Ein weiteres Problem ist die Invertierung von Kovarianzmatrizen von ebenfalls hoher Dimension. Dazu ist die Verwendung zuverlässiger Routinen zur Matrixinversion nötig.
Des Weiteren verwenden wir in unserer Methode ein kompliziertes zweistufiges Iterationsschema, was bis zu 200 Iterationen pro Rekonstruktion nötig macht. Dies bedeutet einen enormen Aufwand an CPU-Zeit, was uns dazu bewegt hat, den Code zu parallelisieren. Zu diesem Zeitpunkt ist er für eine Ausführung auf Computern mit 10-25 Kernen ausgelegt.
Noch einige Worte zur konkreten Gestalt des Programmpakets. Der Code ist objektorientiert in C++ geschrieben. Alle wesentlichen Funktionen sind unabhägig von der Rekonstruktionsroutine aufrufbar und in den dem Code zugrundeliegenden Bibliotheken verfügbar. Für eine ausreichende Anwenderfreundlichkeit ist das Programm durch Konfigurationsdateien zu bedienen und mithilfe eines Makefiles auch einfach zu installieren.
Hier noch kurz eine Auflistung der externen Bibliotheken, die neben der C-Standardbibliothek verwendet werden, und die Beschreibung Ihrer Funktion innerhalb des Programms.

• GNU Scientific Library (GSL)
  Vektor/Matrix Verwendung, Statistik, komplexe Zahlen, lineare Gleichungssysteme, Zufallszahlen.
• Numerical Recipes (NR)
  Zweidimensionale, bikubische Spline Interpolation (wird in Zukunft wohl ersetzt durch GSL).
• Linear Algebra Package (LAPACK)
  Hochdimensionale Matrixinvertierung, lineare Gleichungssysteme
• CFITSIO & CCfits
  Ein. -und Ausgabe mit Hilfe des FITS-Formats.
• Message Passing Interface (MPI)
  Parallelisierung auf mehrere Prozesse.

Der Code selbst ist in unserem Repository verfügbar.