Reconstruction of Galaxy Clusters by Gravitational Lensing

General considerations

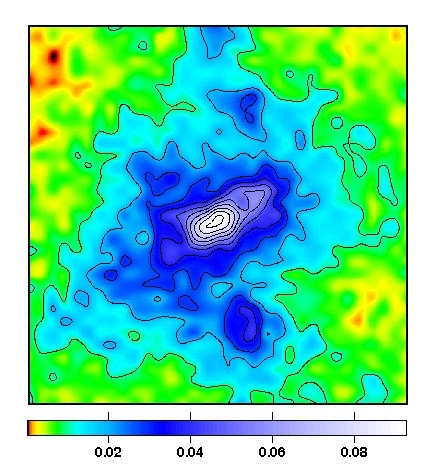The content of our work is the precise reconstruction of the mass profile of a galaxy cluster. As mentioned in the general introduction, galaxy clusters are very important cosmological objects whose abundance in the sky and exact mass has to be determined accurately. In our opinion gravitational lensing is the most promising method for this task.
While strong lensing allows for an highly resolved reconstruction of the cluster core, weak lensing constrains the whole observed field. A combination of both effects, like we suggest in our method, offers the possibility to reconstruct a galaxy cluster on all observed scales.

References

Besides our own publications, also two other methods combining weak and strong lensing are listed here.

• Combining weak and strong lensing in cluster potential reconstruction
  Cacciato, Bartelmann, Meneghetti, Moscardini
  2006, A&A, 458, 349
  [astro-ph]
• Combining weak and strong cluster lensing: Applications to simulations and MS 2137
  Merten, Cacciato, Meneghetti, Mignone, Bartelmann
  2008, submitted to A&A
  [astro-ph]
• Strong and weak lensing united I: the combined strong and weak lensing cluster mass reconstruction method
  Bradač, Schneider, Lombardi, Erben
  2005, A&A, 437, 39
  [astro-ph]
• Combined reconstruction of weak and strong lensing data with WSLAP
  Diego, Tegmark, Protopapas, Sandvik
  2007, MNRAS, 375, 958
  [astro-ph]

The reconstruction method

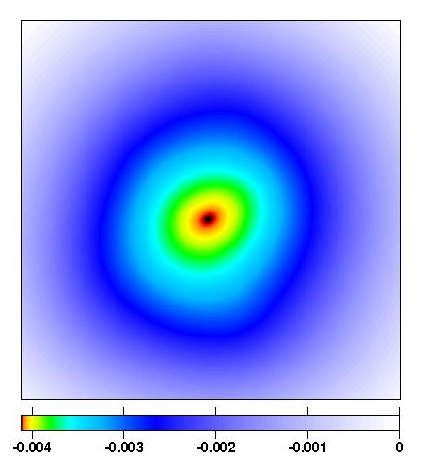We decided to focus on the lensing potential as reconstruction quantity. It is the rescaled and line-of-sight integrated Newtonian Potential. The main advantage of this potential compared to other more direct reconstruction quantities like e.g. the density distribution is its smoothness, which makes it very stable against noise and outliers in the input data.
The basic idea of our algorithm is a so-called maximum-likelihood method, which tries to find the lensing potential that is most likely to have caused the observed effects. To do so, we divide the observed field into pixels and obtain a regular grid. Afterwards, we define a chi-square-function in every pixel and minimise it on that grid. The quantity with respect to which we minimise is the lensing potential itself. While doing so and additionally assigning to every pixel an observational constraint which depends on the lensing potential, we obtain a non-parametric reconstruction method. How this chi-square-function looks explicitly, we explain in the next section.

References

Here a reference to maximum-likelihood based cluster-reconstruction methods.

• Maximum-likelihood Cluster Reconstruction
  Bartelmann, Narayan, Seitz, Schneider
  1996, ApJ, 464L, 115B
  [astro-ph]

Different lensing effects

At this development stage of our algorithm, we use two different lensing constraints in our reconstructions.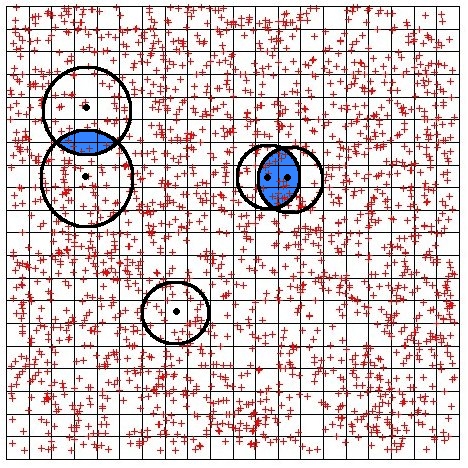 First, there is weak lensing, meaning slight elliptical distortions of the background galaxies. Like described in the article about lensing this effect has to be treated statistically, since the background galaxies also carry intrinsic ellipticity. One can show that the expectation value of the ellipticity is equal to a characteristic lens quantity called reduced shear, which is dependent on second derivatives of the lensing potential. In this way we found the quantity to define the weak-lensing chi-square function. To perform the necessary average over background galaxies, circles around each pixel are drawn, whose radii iteratively increase until a sufficient number of galaxies (usually 10-15) is contained. 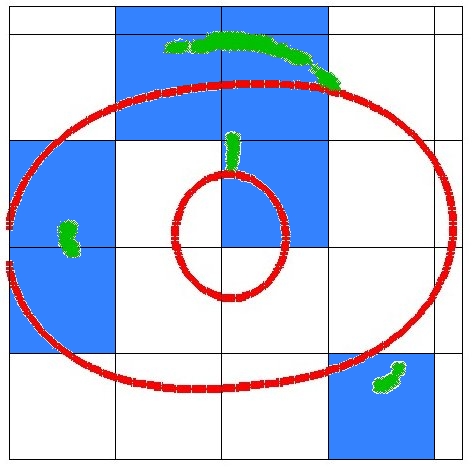The radii of different pixels can overlap, the emerging correlations are taken into account during the reconstruction.
The constraint corresponding to strong lensing are gravitational arcs. Given the resolution is not too high, one can show that these arcs lie closely to the so-called critical curve of the lens. This is another characteristic lensing quantity which also depends on second derivatives of the lensing potential. For every pixel containing parts of an arc, we define an additional chi-square function which takes into account the strong lensing effect. Because these arcs are observable very well and the grid resolution due to the weak-lensing averaging is low anyway, we use a refined grid resolution for these pixels in order to conserve the strong lensing information.

References

A detailed description of the method, including the missing formulas, can be found here.

• Combining weak and strong cluster lensing: Applications to simulations and MS 2137
  Merten, Cacciato, Meneghetti, Mignone, Bartelmann
  2008, submitted to A&A
  [astro-ph]

Advantages of our method

Before we focus on more technical details, we want to point out the main advantages of our method, compared to other concepts.

• The advantage over methods which are limited to only one lensing effect is obvious. A combination of both effects allows a reliable reconstruction on all scales.
• The maximum-likelihood approach makes the method enormously flexible since one can define chi-square functions for many different observations. In fact, right now we are including flexion and multiple image systems.
• The adaptive-averaging scheme for the background galaxies allows for reconstructions on high resolution even with a low density of background galaxies.
• The usage of arcs as strong lensing constraint is very convenient since they are much easier to observe than e.g. multiple image systems.

Numerical implementation

The concrete technical and numerical implementation of the reconstruction method described above is not an easy task. First of all, mostly second derivatives of the lensing potential are appearing in the chi-square function. We represent those by finite differences on the grid, which allows to perform the derivatives by simple matrix multiplications. The problem is that many of these multiplications with a high dimensionality are necessary. Fortunately, those matrices are relatively sparse band matrices, which allow for specialised and extremely fast multiplication algorithms. In practise we achieved an increase in speed by a factor of 1000 while using these algorithms. Another issue is the inversion of also high-dimensional covariance matrices. For this purpose, we use already available and reliable routines for matrix inversion.
Furthermore, we use a complicated two-level iteration scheme, which sums up to a maximum of 200 iterations per reconstruction. This means a high amount of CPU-time, which convinced us to parallelise the code. Right now it is optimised to run on machines with 10-25 cores.
Some additional words on the concrete appearance of the package. The is code object-oriented and written in C++. All fundamental functions can be called independently from the reconstruction routine and are available in the code libraries. To provide basic usability, it can be configured and run by configuration files. For an easy installation there is a Makefile available.
In the end a listing of external libraries used, besides the C standard library, and their function in the code.

• GNU Scientific Library (GSL)
  vector/matrix handling, statistics, complex numbers, linear systems of equations, random numbers.
• Numerical Recipes (NR)
  two-dimensional bicubic spline interpolation (might be replaced by GSL in the future).
• Linear Algebra Package (LAPACK)
  high-dimensional matrix inversion, linear systems of equations.
• CFITSIO & CCfits
  in. -and output in FITS-format.
• Message Passing Interface (MPI)
  parallelising to many processes.

The code is available in our Repository.