Gravitational Lensing

Introduction

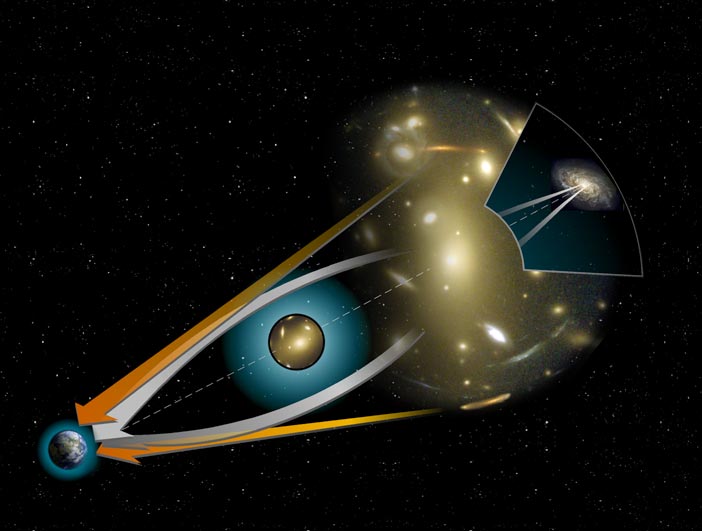As described by Einstein's theory of general relativity, gravitation is a property of space-time caused by the objects it contains. This is why also the pathway of light is affected by massive objects. A light ray which would travel on a straight line, now encloses an angle with this line. This effect is called gravitational lensing and can be deduced by Fermat's principle, in analogy to classical optics. According to this theorem light always travels along the pathway with the smallest delay.
There are three ingredients to a simplified lensing scenario, a source, a lens, and an observer. The connection between those three is given by the lens equation, which describes under which angle the source is seen by the observer with a lens present, in comparison to the observed angle without the lens.
For expanded sources, the effects of an sufficiently strong lens are usually distortion and magnification. In the following we distinguish several effects which are caused by different source-lens configurations.

Microlensing

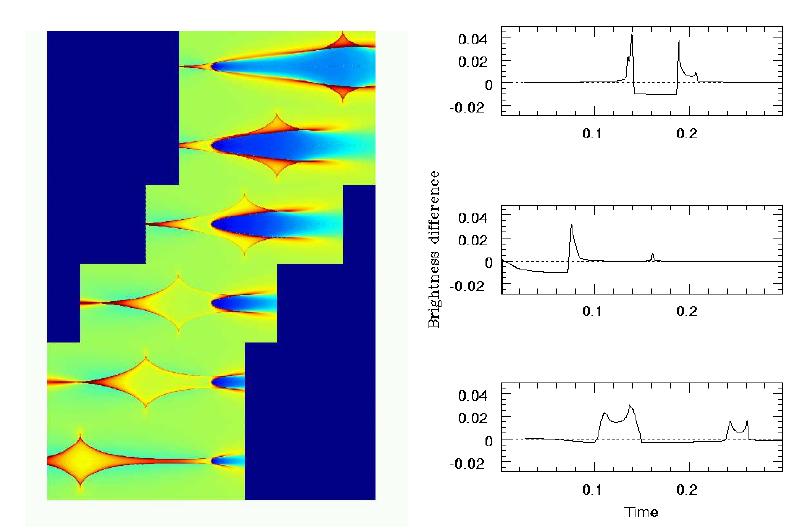Whenever the spatial extent of a lens is small with respect to size of the overall lens system, one is in the regime of microlensing. Typical lenses in this case are planets, stars or other compact objects. Typical observations are magnification effects, which are reflected by peaks in the light curves of the background sources.
The first big application of microlensing worth mentioning was the search for massive astrophysical compact halo objects (MACHOs), which are one of the possible dark matter candidates. But the surveys conducted so far delivered to few observations for a sufficient explanation of the dark matter problem.
Also for the search of extrasolar planets microlensing is a promising method. The special lens configuration of a star and a planet in its orbit produces a very specific light curve of a background star. Out of these light curves one can draw conclusions on the planet in the system.
Finally, microlensing is also used in the observations of quasi stellar objects (QSOs). Often, multiple images of a QSO source appear which give information about the lens, usually a galaxy, and about the QSO.

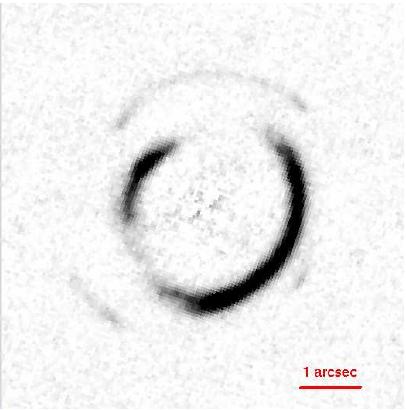
Strong lensing

From now on we focus on much more extended and massive lenses. Examples are galaxies or clusters of galaxies. Near the massive centres of these lenses a phenomenon called strong lensing can occur. Under this keyword one understands very spectacular distortions and magnifications of background sources. One possibility for strong lensing are multiple images of a single source. This is possible since the lens equation allows for several solutions. With an additional spectroscopic analysis of the image, one can assign these multiple objects back to a single source again. An even more spectacular effect is the distortion of almost point-like sources to giant arcs. With an appropriate source-lens configuration these arcs can even become complete rings around the centre of the lens. This is called an Einstein ring. Until now, hundreds of arcs and even a few Einstein rings were identified.

Weak lensing

While strong lensing is well observable, weak lensing, as the name states, is not such a spectacular occurrence. By assuming a background galaxy to be point-like and its emission passing a gravitational lens, it will appear slightly elliptical. Typical ellipticities are of the order of a few percent. Because this effect is not limited to the centre of a lens, observations over a larger fieldsize are possible. At the same time, weak lensing is a statistical process since the background galaxies carry intrinsic, but randomly orientated ellipticity. For this reason high source density is important in order to average out these unwanted systematic effects.
Typical lenses in weak lensing are galaxies or galaxy clusters, but one also observes so-called cosmological weak lensing. In this case, one observes huge field sizes and makes use of statistical methods to quantify the lensing effects by the large-scale structure in the universe. This is a very direct test of cosmological models. Furthermore, the shape of the cosmic microwave background is slightly altered by the large-scale structure as well.

Literature

Here are some suggestions for further reading:

• Schneider, Kochanek, Wambsganß und Meylan; Gravitational Lensing: Strong, Weak and Micro; 2006 Springer
• Massimo Meneghetti, Introduction to Gravitational Lensing, 2006 lecture notes, University of Heidelberg
  [pdf]
• Joachim Wambsganß, Gravitational Microlensing, 2006 Proceedings of the 33rd Saas-Fee Advanced Course
  [astro-ph]
• Matthias Bartelmann und Peter Schneider, Weak Gravitational Lensing, 2001 Physics Reports 340, 291
  [pdf, NASA ADS]